複利効果の実際　半年複利と1日複利の違いは？ - FIRE: 投資でセミリタイアする九条日記

投資の世界では、「複利効果」が大事だといつも言われます。アインシュタインが「歴史上最大の数学的発見」と言ったというほど大事なことです。でも、複利の効果はどのくらいあるのでしょうか？

複利の威力というと、よく30年投資したときに、単利と複利ではこんなに差が開きます、というような話がでてきます。もうこれは常識的な話ですね。でも今回考えてみたいのは、複利が効果的だというのなら、複利計算が行われる頻度が高いと、どのくらいの効果が上がるのか？　ということです。

例えば、貯金の利子や個人向け国債では半年ごとに利息が支払われます。この利息を再投資したとすれば、これは半年複利ということになります。いくつかのETFや投資信託では、年に4回、分配金が出ます。これは同様に3ヶ月複利ということですね。

Poloniexの仮想通貨のレンディング（貸出）サービスは、2日ごとに利息とともに元本が戻ってきます。こちらは、2日複利となり、年に182回再投資ができることになります。

この複利の頻度が上がると、どのくらいメリットがあるのでしょうか？

これまたよく言われるのは、この複利計算の回数をものすごく増やして、無限回にしたときに、複利の効果は自然定数の底であるeになるということです。連続複利といいます。eは、2.7182…… という数字なので、何かの2.7182……倍になることになります。

年間利回り100％の商品があったとします。1の元本を投資したときに、1年後には2になっています。この複利回数を増やしていったら、いったいいくつの数字になるのか。その答えが、2.7182……ということです。つまり、100％が171.82％まで上昇することになります。

ここまでは検索するとすぐに出てきます。では、この上昇の仕方はどんな感じなのでしょう？

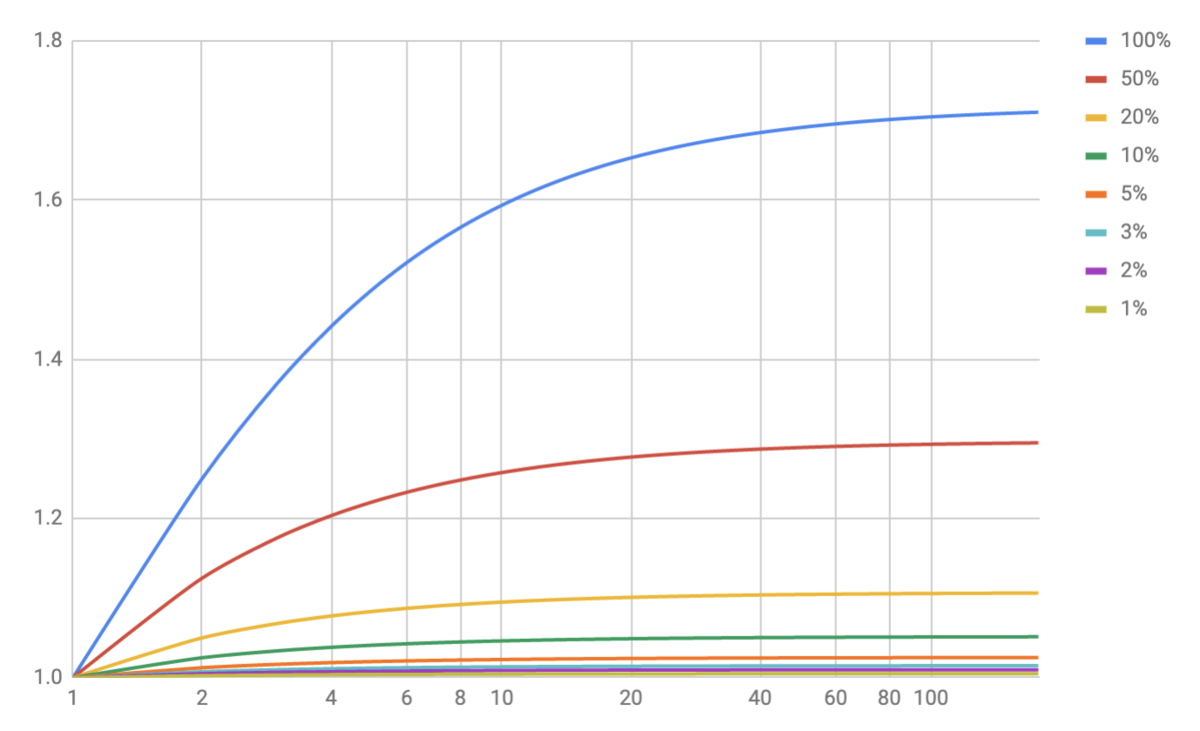
eを使わずとも、( 1+ r/m)^m（rは金利、mは複利回数）という式で、複利計算は表されます。このmが無限大になると、2.7182……＝e になるわけです。ではどのくらいのペースでeに収束するのでしょうか。

f:id:kuzyo:20190528000354p:plain

まずは金利100％の青い線を見てください。複利回数が年に1回だと2ですが、複利回数が増えると一気に増加するのがわかります。だいたい年に11回の複利回数で2.6を超え、19回で2.65を超えます。2.7に達するのは74回です。

2日複利である年182回の複利回数だと、2.7108となります。e の値までは、0.007程度足りませんが、かなり近づいているのがわかります。1日複利である365回だと、2.7145です。ここまで来ると、頻度が倍になっても0.004しか効果は上昇しません。

いったい複利回数がどのくらい増えると、どのくらいの効果になるのでしょうか。今度は、複利回数が1回増えたときに、利回りがどのくらい増加するのか見てみます。

f:id:kuzyo:20190528002405p:plain

金利100％の青い線を例にとると、1年に1回の利払いの場合は増加は1、＋100％です。これが半年複利の2回になると、125％相当にリターンが増加します。その後、10回で159％に達しますが、そこから増加ペースはゆるかやになっていきます。上のグラフでは横軸が対数となっているのに注意してください。

視点を変えて、複利回数を倍、倍、倍としていったときのグラフです。

f:id:kuzyo:20190528003025p:plain

金利100％の青い棒をみると、複利回数8〜16回あたりを境に、ほとんど利回りの増加が見られません。512回複利の段階で2.716です。無限回複利にするとe＝2.7182ですからかなり近づいているのがわかります。

今度は、複利回数を増やすと、利回りが何倍になるかを見てみます。

f:id:kuzyo:20190528003958p:plain

金利100％の青い棒をみると、複利回数2回で25％利回りが増加することがわかります。125％の利回りになるということです。金利50％の赤棒をみると、複利回数を2回にしても、12.5%しか増加しません。これは62.5%になるという意味ではなく、50％の＋12.5%で、56.25%という意味です。

もとの金利が小さくなると、複利効果は急速に失われていきます。金利が5％まで下がると、2回複利にしても5％の＋1.2％しか増加しませんし、32回以降、＋2.5％の増加でほぼ天井です。具体的な金利でいうと、4回で5.095%で、128回でも5.126%です。

なるほど、もともとの金利がそこそこ大きいときは、複利回数を増やすことで利回りは上昇します。金利100％ならば171％程度まで上がることがわかりました。ところが、もともとの金利が小さいと、複利計算回数を増やしてもほとんど効果がありません。

f:id:kuzyo:20190528005508p:plain

このグラフは、金利1％〜3％について、複利回数を512回まで増加させたものです。グラフにしても、ほとんど何が違うのかわからないと思います。ほぼ、効果がないということです。

普通に考えてみると、複利が効果を持つのは、利息に対してさらに利息がついていくからです。ところが、そもそもの利息が小さければ、それに対する利息は誤差レベルまで減少します。

つまり、少なくとも年利50％程度の利回りがなければ、年間の複利回数を増加させても、ほぼ影響はないということです。

最初の例でいうと、預金利息の分配が毎月や毎日になっても、ほぼ最終利回りには影響しません。仮想通貨のレンディングは、2日満期でそのたびに利子が支払われるため、複利効果の恩恵を受けるとなんとなく思っていましたが、数パーセントの利回りでは、ほとんど関係ないことがわかりました。

複利効果が意味を持つのは、長期間に渡って運用した場合の話であり、半年複利や毎月複利であっても効果は薄いということですね。