今日は久々にFIRE、セミリタイアネタを。FIREを目指すにあたって最も悩み心配するのは、果たして死ぬまで資金が持つか? でしょう。それに年金を組み合わせることで、無駄に多くの資産を構築せずに済む方法を考えます。
前提となる考え方
FIREの基本概念は、資産を構築して働かなくても生きていける状態を達成(FI)し、働くかどうかを自由に選択できる(RE)ようになることです。そのためには、資産からの収入だけで食べていけることが必要です。
ではどれくらいの資産があれば、働かなくても生きていけるのでしょうか。重要な変数は「生活費の額」と「運用リターン」です。生活費が多ければ多いだけ資産額も必要になりますし、運用リターンが高いほど必要な資産額は小さくなります。
ただし運用リターンをコントロールすることはおすすめできません。運用リターンを高めようとすると(高めようと思って高められる人であっても)、代わりにボラティリティ(リスク、価格変動率)が増加します。統計的にいうと、複利運用を行っていく中では、ボラティリティが増加すると平均値よりも最頻値や中央値は下がります。つまり、期待したほどのリターンが出ない可能性が高まるということです。
そこで過去データを元に、このくらいの運用リターンなら無理なく可能で、死ぬまで資産が持つ……という研究がされてきました。最も有名なのがトリニティ大学で行われた「トリニティ・スタディ」です。ここでは、過去の運用データを元に、取り崩し率が4%ならば、100回に98回は死ぬまで資産が持つことが示されています。
取り崩し率4%というのは、最初の資産額の4%の額を、毎年ずっと取り崩すという意味です。取り崩し額=生活費だと考えると、最初の資産が生活費の25倍あれば、死ぬまで資産が持つわけです*1。
日本には年金がある
ただし、ここには年金が考慮されていません。日本には公的年金という制度があり、これは死ぬまで受給できるという、長生き保険的な意味合いを持っています。年金が破綻するとか、年金制度が減額になるという話は以前からありますが、まずはそれをおいておいて、現在と同じように継続できる前提で考えてみます。
通常年金は65歳からの受給ですが、これを繰上げたり繰下げたりできます。繰上げて60歳からもらうと、月額が約24%減少します。逆に繰下げて75歳からもらうと84%増加します。
繰り下げると額が増えますが、早死して受給額が減る可能性があります。平均寿命で考えると、何歳からもらうのがよいか? という観点もあって、以前それを試算した記事を書きました。
しかし、本来年金というのは保険です。正式名称が「年金保険」であることからもわかるように、長生きというリスクに対する保険なのです。そこで、本来の長生きリスク対策として考えてみましょう。
長生きリスクを年金でカバーする
FIREにしても老後資金にしても、最も怖いのは死ぬ前に資産が尽きてしまうことです。最も確実なのは、資産を取り崩さず、資産から生まれるお金だけで生活することですが、それにはものすごい額が必要になります。一方、取り崩していくとなると市況状況だけでなく、確率計算上も、「30年はもつけど40年は厳しい」なんて数字が出てきます。
多くの場合「まぁ100歳まで生きると見積もれば大丈夫だろう」とエイヤで考えて、残りの年数を算出します。いま50歳ならば残り50年という感じです。このとき、資産の4%に当たる額(資産1億円なら400万円)を毎年取り崩していくとどうなるでしょうか。
米国株50%、米長期債50%のポートフォリオで、インフレを考慮しつつ、過去データを元にしたモンテカルロ・シミュレーションを行うと、50年後も資産が残っている確率(Success)は76.65%になります。
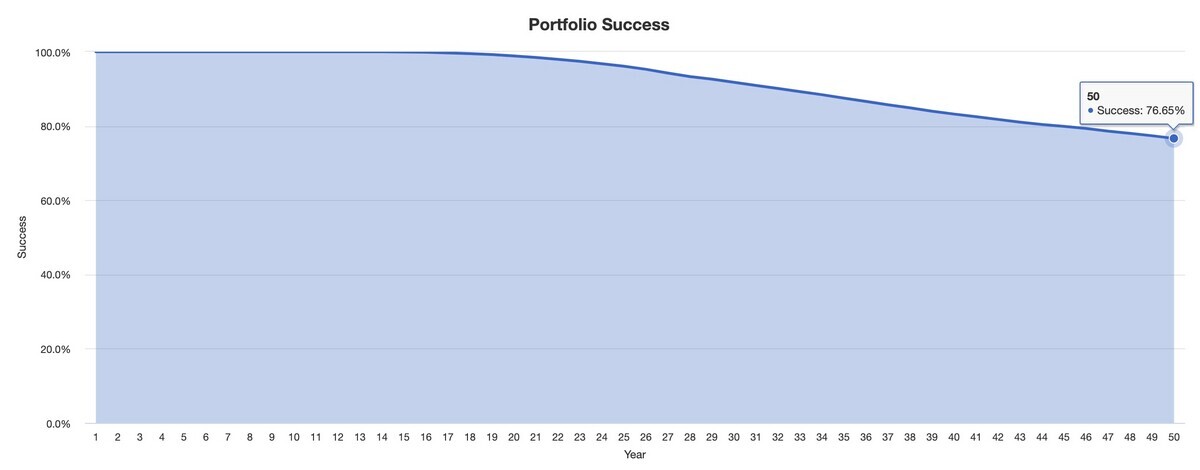
これは決して危険な賭けではなく、中央値(50th Percentile)では50年後、資産がゼロになるどころか約1.5倍に増加しています。それでも、失敗確率が25%近くあるということです。
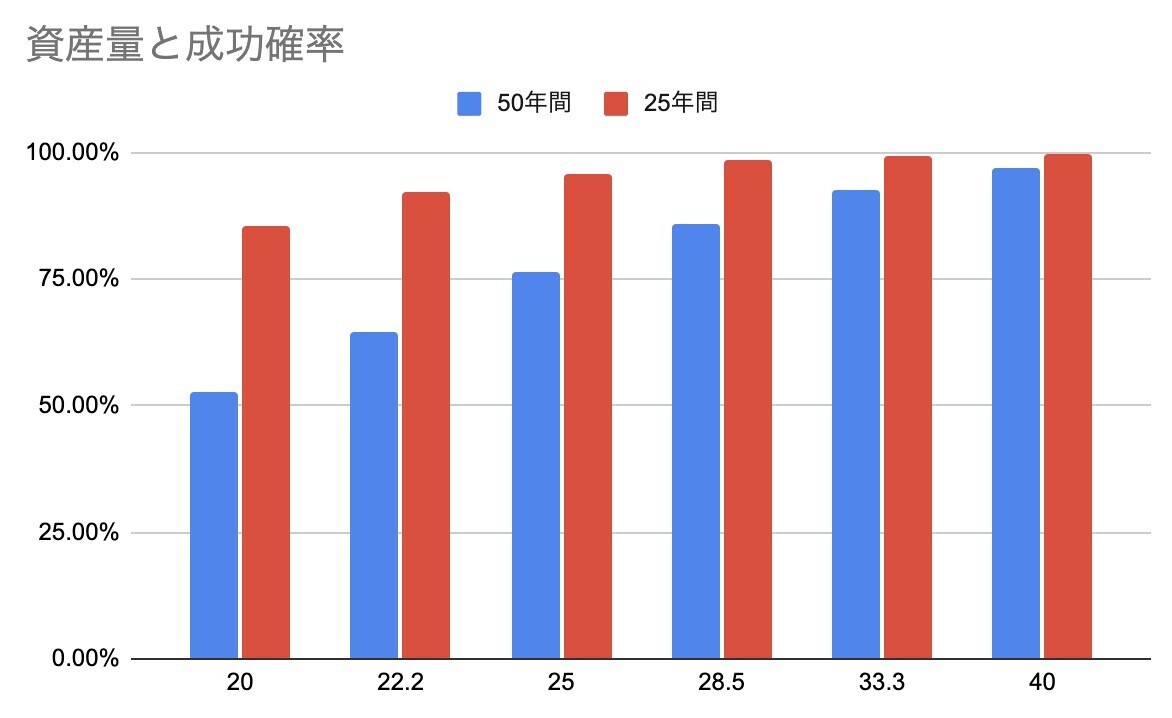
同じ条件で取り崩し比率を減らしたら、成功確率はどうなるでしょうか。最後の倍率は、取り崩し額の何倍の資産が必要かという倍率です。つまり成功確率を97%までもっていきたいなら、確率的には年間生活費の40倍まで資産を貯めなくてはならないということです。
- 5% 52.64% 20倍
- 4.5% 64.44% 22.2倍
- 4% 76.65% 25倍
- 3.5% 85.99% 28.5倍
- 3% 92.57% 33.3倍
- 2.5% 97.13% 40倍
でも、例えば「資産で生きるのは75歳まででOK」と予め分かっていたらどうでしょう? 今50歳なら残りはあと25年間でいいとなったら? このように、4.5%の取り崩しでも成功確率は90%以上に跳ね上がるのです。
- 5% 85.64% 20倍
- 4.5% 92.17% 22.2倍
- 4% 95.96% 25倍
- 3.5% 98.41% 28.5倍
- 3% 99.55% 33.3倍
- 2.5% 99.86% 40倍
グラフにするとこんな感じ。資産寿命を50年もたそうと思うと成功確率を90%以上にするには年間生活費の33.3倍の資産が必要ですが、25年間でよければ22.2倍で済むのです。
そう、年金を限界まで繰下げ支給にして額を増やし、本当の長生きリスクは年金でカバーする。そして、年金受給までは手持ちの資産を活用していく。この方法なら、そこまで巨額の資産を貯めなくても大丈夫となるのです。これぞ、長生き保険としての年金の最適な活用法ではないでしょうか。
反論を考えてみる
年金受給を75歳まで繰り下げて、そこまで資産の取り崩しで生活し、75歳以降は年金ですごす。この方法に対して、どんな反論があるでしょう。
一つは、75歳になったときに年金がもらえなくなっているかもしれないのに資産がなくなってしまうのは不安というものでしょう。ここには2つの仮定があります。1つは年金は本当にもらえなくなるのか? ということ。そして2つ目は、75歳のときに資産はなくなっているのか? ということです。
1つ目は政治的な話であり、確率的に議論できるものではありません。なのでこの考察はまた別の機会に。
そして2つ目です。成功確率が90%だといっても、その時資産がゼロになっているわけではないのです。下記は、25年間4.5%に当たる額を取り崩し続けたときの資産額の推移です。下位10%(10th Percentile)ではたしかに資産額が当初よりも減少してしまっていますが、下位20%よりも上では資産は減るどころか増加しています。中央値にあたる50th Percentileでは2.8倍に増加しているのです。
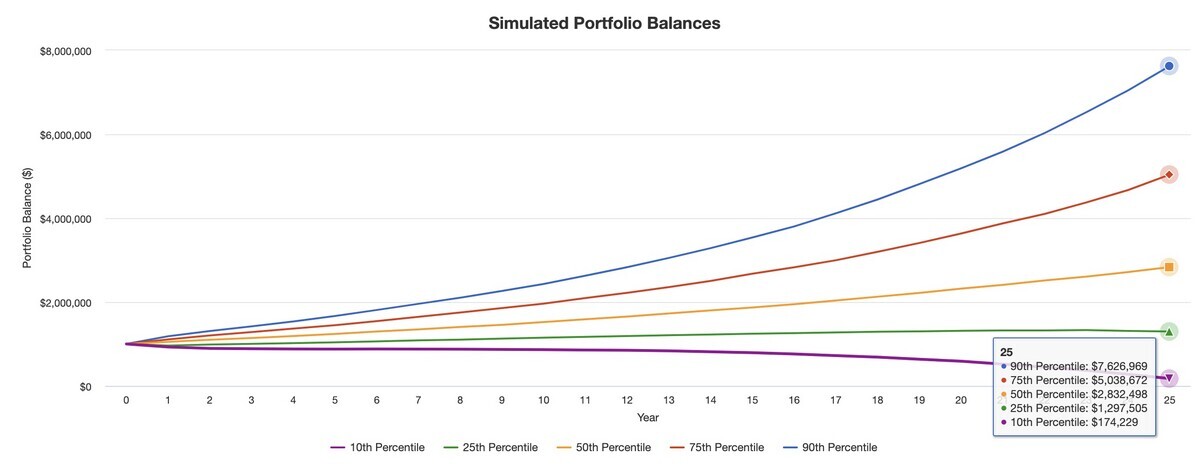
25年後の成功確率が9割以上になるレベルの取り崩しを行ったとしても、ほとんどの場合、資産はぐんぐん増加しているのです。
つまり、75歳以降は84%増しの年金があるからそれでなんとかなるだろうと思えれば、4割少ない資産でなんとかなります。そしてそれはあくまで万が一の保険であって、ほとんどの場合は資産が75歳のときに尽きているなんてこともないのです。
※本当は、年金を65歳からもらう場合と75歳からにした場合で、必要資産額と成功確率がどう変わるかを検証したかったのですが、今回はざっくりとした概念の話で。そのうち、計算もしてみたいと思います。
*1:よくある誤った説明のように「4%で運用すれば永遠に資産が減らない」という意味ではないことには注意です。