投資資金が2倍になるまでの年数を暗算できる「72の法則」は有名です。ところがこれの積立投資版は複雑で、これまで聞いたことがありませんでした。ところが、慶応大学の枇々木規雄教授の論文「126ルール:積立投資の複利効果を概算する簡単な計算ルール」には、積立投資で投資額が2倍になるまでの年数や利回りを暗算する方法が書かれています。
72の法則
72の法則は簡単です。これは投資資金が2倍になるまでの期間と利回りの関係が次の式になるということを表しています。
- 投資期間 × 利回り = 72
例えば、100万円を利回り6%で運用すると2倍になるのに何年かかるでしょう? これは
- 投資期間 × 6 = 72
なので、72を6で割って12年だと分かります。では100万円を40年運用して2倍にしたいなら、どのくらいの利回りが必要かというと、72を40で割って1.8%が必要だと分かるという具合です。
実際に計算すると、
- 6%で12年運用すると→2.01219647184となり、ほぼ2倍です
- 1.8%で40年運ようすると→2.04132013821となり、こちらもほぼ2倍です
とこのように簡易ながらとても使い勝手のいい法則でした。なお3倍については下記に書いた「115の法則」で同じように求めることができます。
積立投資の場合
72の法則や115の法則は比較的導出や証明も容易なのですが(Webで検索してください)、積立投資はなかなか難しい。これを同様のやり方で暗算できるようにしたのが枇々木規雄(ひびきのりお)教授の「126の法則」です。
使い方は同様で、
- 投資期間 × 利回り = 126
として使います。前提は毎月同額を積み立てて運用した場合です。例えば、毎月1万円を20年間積み立てて運用したとします。積立額は年間12万の20年分で240万円。これが2倍になるには、
- 20 × 利回り = 126
で6.3%の利回りが必要だと計算できます。また、4%の利回りで運用した場合、積み立て総額の2倍になるのは、
- 投資期間 × 4% = 126
で、31.5年が必要だと分かります。
枇々木教授は126の法則を利用して、積立の効果をつぎのように書いています。
23歳から65歳まで42年間働くとして、働き始めてからすぐに積立投資を始め、平均的に年率3%で投資できるが、おおよそではあるが積立額は半分で済む(2倍になる)と考えるとわかりやすいだろう。
ちなみに、複利ではなく単利の世界で、満期額が積立元本の2倍になるのはおおよそ「年数 × 利率 =200」だそうです。これが126で済むのですから、複利の効果は非常に大きいことが分かります。
2倍以外の「3倍になる190の法則」「1.5倍になる76の法則」
枇々木教授は2倍だけでなく、1.333倍、1.5倍、2.5倍、3倍のそれぞれを計算しており、下記のようにルールを論文にまとめています。
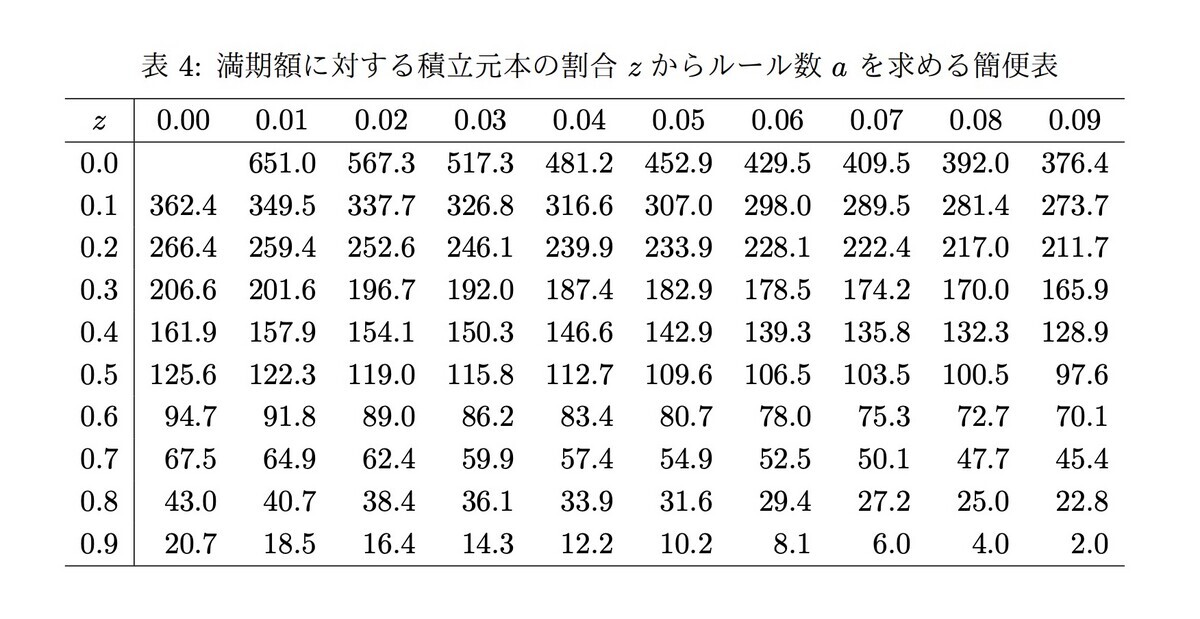
さらに詳細なルール数について、下記の表にまとめています。zは「満期額に対する積立元本の割合」を示すので、0.5なら2倍になったことを意味しますし、0.2なら5倍になることを意味します。