この数年で「長期・分散・積立」が本当に普及しました。これは「つみたてNISA」「クレカ積立」「インデックス投信」「ロボアド」などの効果によるものだと思っています。しかし、一つだけ「積立」についてはいろいろと誤解されていのではないか？ と思っています。
長期・分散・積立の意味
金融庁が旗をふった長期・分散・積立コンセプトはかなり普及しました。最初にこれらの意味をざっくりと捉えておきましょう。
長期というのは長期投資です。これは金融商品への投資は短期間では減ることもあるけれど、長期間投資すると増えることが多いというものです。これは2つの意味あいがあって、1つは過去実績（エビデンス）によるもの。2つ目は理論（ロジック）によるものです。長期投資すれば、理屈上も実績上も損することなく資産が増加するというわけです*1。
分散というのは、1つの商品だけでなく複数の商品に投資するということです。こちらは現代ポートフォリオ理論の中で理論化されていて、互いに値動きが相関しない資産を組み合わせると、リターンは平均になるのにリスクは平均よりも低下するというものです。
具体的には、株式インデックスへの投資であり、債券や金、不動産などを組み込んだロボアド的なポートフォリオを組むということです。
この長期と分散は、理論上も実績上も効果があることが分かっています。投資の定石であり常識でもあるわけです。ところが、「積立」についてはいろいろと難しいのです。
積立のよく言われるメリット
積立投資は、毎月など定期的に金融資産を買い付けていく投資法です。この利点は次のように言われています。
- 感情に左右されない
- ドルコスト平均法で買い付けられる
（1）の感情に左右されないのは本当に重要です。価格が下落したら弱気になって売りたくなるし買付を止めたくなり、価格が上昇したら強気になってもっと買いたくなったりするからです。
ところが、「ドルコスト平均法」については少々疑念があります。いつでもどんなときでもドルコスト平均法がベストかのように考えると、理論的な投資のベストプラクティスから離れてしまう可能性があります。
ドルコスト平均法
まずドルコスト平均法のメリットとして、定量購入と比較した図がよく出てきます。下記のようなものです。これは、「一定額」ずつ買うのと「一定量」ずつ買うのでは、一定額のほうが単価が安く済むという話です。一定額購入＝ドルコスト平均法なので、お得だと言われます。
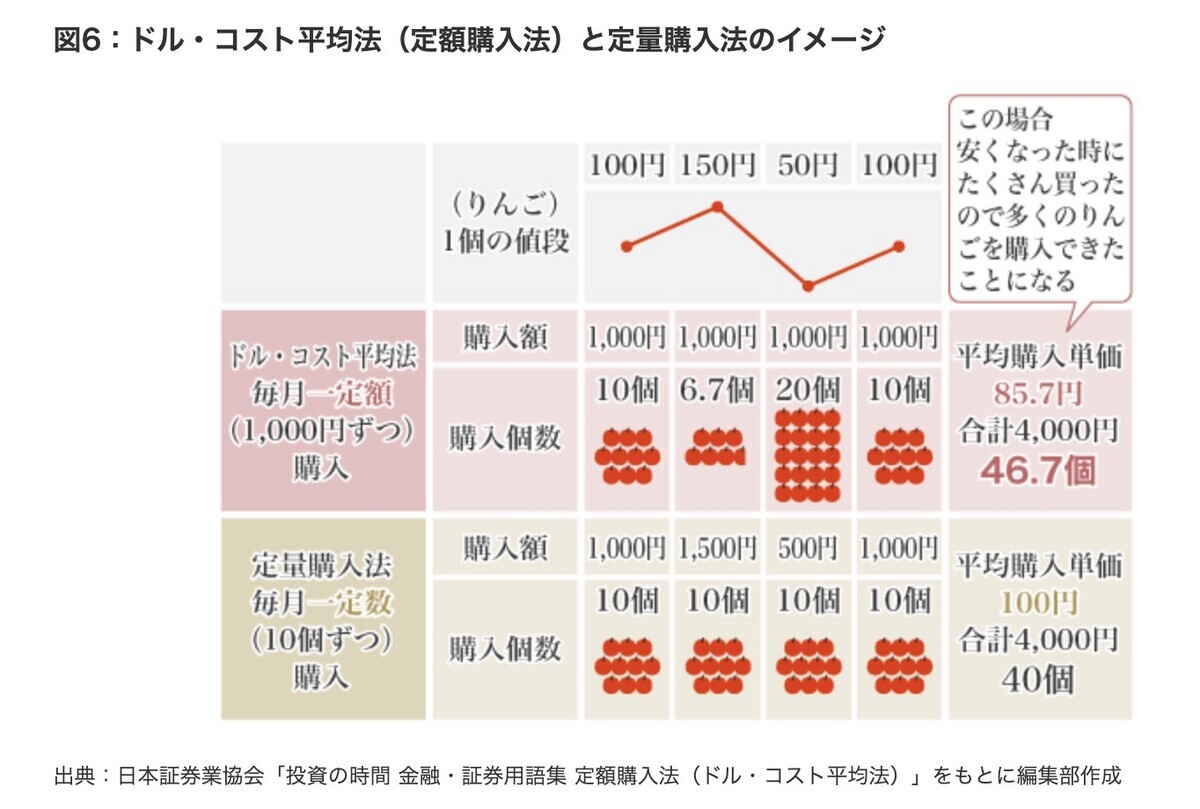
これは理論的には正しい内容です。これは一定数の購入が相加平均なのに対し、定額買付が調和平均となるためです。数学的に、相加平均（算術平均）≧相乗平均（幾何平均）≧調和平均となるため、どのような場合でもドルコスト平均法のほうがお得になります。
でも果たして「一定量」で買付なんてするでしょうか？ 毎月1万円ずつ投信を買うならあっても、毎月10口ずつ投信を買うなんてことは普通はしません。投資はおやつのリンゴではないからです。だれもしない手法と比較して安く買えるといっても、これはちょっと違いますね。
積立vs．一括
もう一つ、多くの場合で問題になるのが「一定額積立」と「一括投資」の比較です。金融庁の資料には下記のように例をあげて「一括より積立のほうがお得」としています。正確には「この例では平均購入単価を安くすることができた」としていますが、明らかにミスリードです。
どういうことでしょうか。
この例では、一括が単価1万円で買い付けています。ところがその後、半値まで値下がりしたタイミングがあったためにたまたま安く買えました。と、ただそれだけの話です。一般論として、
- これから値上がりしていくなら一括投資が有利
- これから値下がりするならドルコスト平均法が有利
となります。ちなみに価格が変動した場合も、下記の3パターン（Aは金融庁の例）を考えてみましょう（いずれも算術平均価格は1.125）。
実は、Aの値動きだと購入口数が4.5口と一括の4口より大きくなりますが、B、Cでは一括よりも少なくなります。
- A 4.5口
- B 3.71口
- C 3.63口
単純に値上がりしていくパターンだけでなく、上下していてもその形によってドルコスト平均法の有利不利は変わります。
モンテカルロ・シミュレーション
本当は確率的に計算できればベストなのでしょうが、この形の計算はけっこうややこしいらしく、ほとんど見ることがありません。こういう場合はモンテカルロシミュレーションです。
下記のブログにモンテカルロ・シミュレーションをやってみた結果が掲載されていました。年金基本ポートフォリオの期待リターン4.57%、リスク12.8％でのシミュレーションです。
ここでは、リスクとリターンを分けて出していて、ドルコスト平均法のほうがリターンもリスクも小さくなっています。それは当然です。一括投資が現金を持たずにすべての資産をリスクに晒しているのに対し、ドルコスト平均法ではざっくり半分は現金で保有しているからです。
そこでリターンをリスクで割ったシャープ・レシオでも見てみましょう。面白いことに、期間が長くなるほどシャープレシオは向上しますが、ドルコスト平均法と一括投資ではほぼ数字が一緒です。多少違いますが、これはシミュレーションがゆえの誤差です。
ここから分かることは下記の2つです。
- ドルコスト平均法は買付単価を下げない。下げているならリターンが改善するはず
- ドルコスト平均法はリスクを下げない。下げているならリスクが減少するはず
つまり、ドルコスト平均法は投資前半にだけ現金を手元に置いておくという以上の効果がないということです。
リスクに晒す資金の量で考える
別の視点でも考えてみましょう。下記の2つのどちらが有利だと思いますか？
- 100万円を今投資する
- 100万円を1年後に投資する
1年後の価格が上がっているのか下がっているのかが分からない以上、どちらも同じだと考えてしまう人もいるかもしれません。ところがそれは誤りなのです。投資（ここでは株式や債券などの伝統的な投資）が期待値がプラスである限り、少しでも早く投資を行ったほうが有利なのです。いわゆる時間価値というものです。
これは、下記の2つのどちらが有利かを考えるとよく分かります。（2）は要するに「投資しない」という選択肢と同じなのです。
- 100万円を今投資する
- 100万円を30年後に投資する（そこまで現金で持っておく）
では積立投資とは何でしょうか。下記を考えてみましょう。1−1はいわゆる一括投資です。そして1-2は積立投資です。
- まず50万円を今投資する
- 残りの50万円も今投資する
- 残りの50万円は1年後に投資する
これを見ると、1-2の積立投資が、50万円について単に1年間「投資しない」という選択を取っただけだということが分かります。
これは1年おきに2回に分けて積み立ててみましたが、もっと頻度が多くても同じです。積み立て投資というのは、投資タイミングを遅らせるだけのもので、その間投資しないで現金で保有することを選択している投資法に過ぎないのです。
別の言葉でいうと、投資の成果はリスクに晒している資金量とその期間に応じて決まります。価格の変動が予測できず、ただし期待リターンがプラスならば、自然とそうなるのです。ところが、積み立て投資は一括投資に比べて、リスクに晒す資金量を減らす行為です。そのため成果も減ることになります。
別の弊害もあります。それは投資を始めた初期は資金量が小さく、後期には資金量が大きくなることです。これは初期の好調な市況の恩恵を受けられず、後期に暴落があったら大損害となります。市況は平均するとプラスですが、好調が先にくるか暴落が先にくるかは分かりません。一括投資であれば、その影響は平均されて均されますが、積み立て投資の場合、先に暴落が来たほうが有利で後に暴落が来ると壊滅的です。いわゆるシーケンシャルリスクを受けることになるのです。
だから新NISAでは一括投資
こうした理論・実績的な背景があって、枠が年間360万円に拡大される新NISAでは、一刻も早く枠を埋めるのがベストだと考えています。もちろん、含み益がある特定口座からの乗り換えは税金を考慮しなくてはいけませんし、負担できるリスクを超えて手持ちの現金を新NISAに入れろといっているわけでもありません。
投資しようと考えている現金があるのに、360万円を少しずつ埋めていったほうがいいというドルコスト平均法の呪いにかかってはいけないという話です。それなら一括投資するのが理論的には有利です。
なおドルコスト平均法が意味を持つ場合もあります。それは取り崩しのときです。取り崩しのときは、一括取り崩しを考える人はあまりおらず、定額取り崩し＝ドルコスト平均法か、定率取り崩しを検討すると思います。
ところが、相加平均（算術平均）≧相乗平均（幾何平均）≧調和平均という数学的事実からドルコスト平均法に当たる定額取り崩しは、どんな相場であっても不利になります。調和平均だからです。ここは相加平均である定率取り崩しがベストなわけです。
ちなみに手元に現金がない場合の投資法は、当然ながら積み立て投資一択です。リスクに晒す資金量を多くすることが投資の成果を増やす理論的な解なので、貯めてから一括投資なんてやってはいけません。給与から積み立てるなら、積立額は一定に近くなるはずで、そういう意味では積立投資がベストなのです。
*1:ちなみに長期投資ではリスクが減少すると言われますが、そのリスクが何を指すかを厳密に定義しないと、実はリスクが減っていなかったりします。長期投資で確実に改善するのは年平均リターンですが、確率的にいえば意外と複雑です。つまり、期待リターンと最頻値と中央値はそれぞれ異なり、さらにリスク＝ボラティリティによってその変化度合いも変わるのです
