ロジカルに投資を捉えている人の多くは「期待値がプラスであること」を最重視しています。例えばギャンブルは胴元の取り分が多く、期待値はマイナスですね。一方で、長期株式投資は企業の利益が積み上がることから期待値はプラスになります。では、そのほかのさまざまな投資手法において、期待値がプラスならば投資に値するのでしょうか?
- サンクトペテルブルクのパラドックス
- 株価変動が正規分布に従うとしたら
- 期待値(平均値)と中央値と最頻値
- リスクを下げると中央値も最頻値も改善する
- 平均値(期待値)をアテにすると誤る可能性がある
- モンテカルロ・シミュレーションでも確かめる
サンクトペテルブルクのパラドックス
ここで期待値が無限大になる賭けの例を見てみます。サンクトペテルブルクのパラドックスと呼ばれるものです。
偏りのないコインを表が出るまで投げ続け、表が出たときに、賞金をもらえるゲームがあるとする。もらえる賞金は、1回目に表が出たら1円、1回目は裏が出て2回目に表が出たら倍の2円、2回目まで裏が出ていて3回目に初めて表が出たらそのまた倍の4円、3回目まで裏が出ていて4回目に初めて表が出たらそのまた倍の8円、というふうに倍々で増える賞金がもらえるというゲームである。
このギャンブルの期待値を計算すると、驚くべきことに無限大の期待値となります。ならば、有り金のすべてを突っ込んで投資するべきなのでしょうか? ところが、1円がもらえる確率は2分の1、2円がもらえるのが4分の1、512円がもらえる確率は1024分の1しかありません。
つまり、たいていはほとんど儲からないが、ごく稀にものすごい儲けが出るために、期待値としてはプラス(どころか無限大)になるわけです。
モンテカルロ・シミュレーションを行い、大量の試行をしたときの結果が下記のブログに載っていました。

1,000,000,000回(10億回)以上やるつもりなら、1回あたり10円以上儲かることがほぼ確実
とあるように、ものすごい回数をこなしても確実に儲かるのは10円程度ということです。この結果をどう捉えるかですね。
株価変動が正規分布に従うとしたら
株価の変動率は正規分布に従うという仮定の元に、多くの金融理論は成り立っています。つまり平均リターンが6%で、変動率の分散(σ)が20%だとすると、年率リターンは下記のように分布するということです。
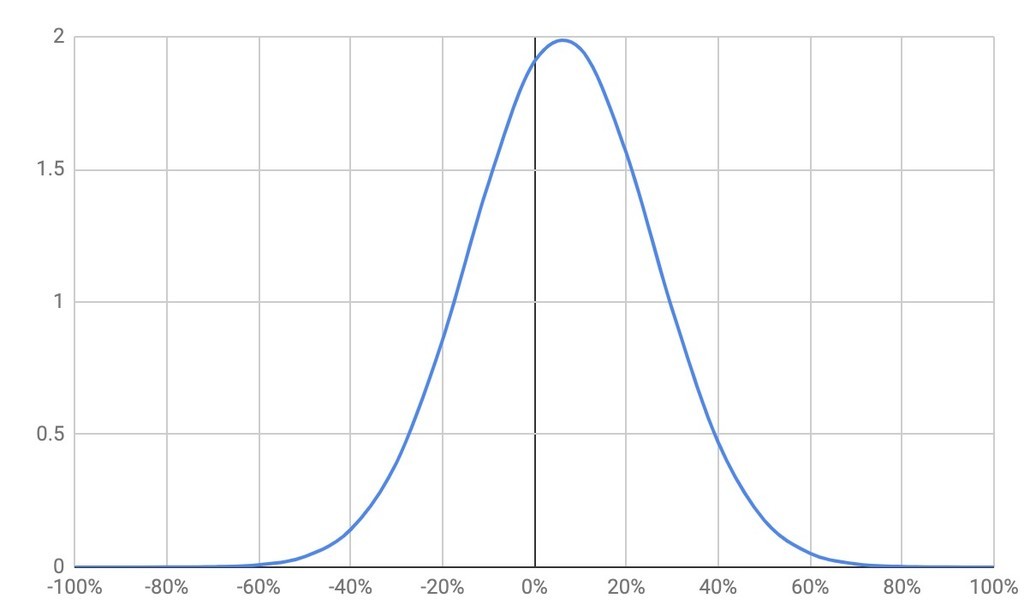
そして変動率が正規分布に従うとすると、株価自体は対数正規分布になります。対数とついているのは、正規分布グラフの横軸として対数を取ったときにできるグラフだからです。

※縦軸はスケールが違うので、あくまで分布の形を見てください
赤い線が対数正規分布です。この特徴は、平均値は同じく6%なのに、確率密度は6%よりも低いところが最大になっていることです。別の言い方をすると最頻値や中央値は6%を下回ります。
これは何を意味するのでしょう? 株価の変動率が正規分布に従うとしたら、株価の動きは対数正規分布になります。そして対数正規分布のグラフでは、平均値は確かに6%ですが、多くの場合、6%を下回るということです。もっといえば、ほとんどの人は6%のリターンに届きません。ただし、平均すると6%になるということです。
期待値(平均値)と中央値と最頻値
これが意味することは結構重要です。複利運用を続けた場合に、期待値(平均値)は想像通りに上昇しますが、中央値と最頻値は思ったようには上昇しないからです。期待例ターン5%、リスク20%(分散、σ)を前提として、こちらのサイトに計算したものがありましたので、引用します。

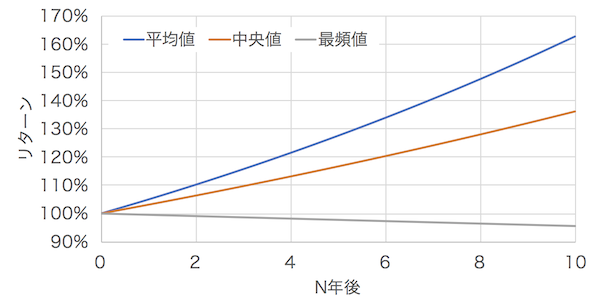
長期に渡って複利運用を続けた場合、確かに平均値は上昇します。これは想定どおりです。しかし中央値は平均の伸びに及びません。つまり、半数の人はこの中央値リターンを下回るということです。平均以下が半分ではないことに注意が必要です。
さらに、最頻値はなんと100%を下回ります。つまり、最も可能性が高いシナリオは元本割れということです。これが数学的な結論です。
普通は、平均値を前提に10年運用すればこのくらいの金額になる、と考えがちです。ところが、半分の人は中央値を下回ります。そして、最も多い可能性は元本割れだというのです。これがリスクの問題です*1。
リスクを下げると中央値も最頻値も改善する
そして、リスクを下げると、中央値も最頻値も改善することが分かります。同じく、こちらのサイトに計算したものがありましたので、引用します。このグラフは、期待リターン3.5%、リスク10%としたものです。

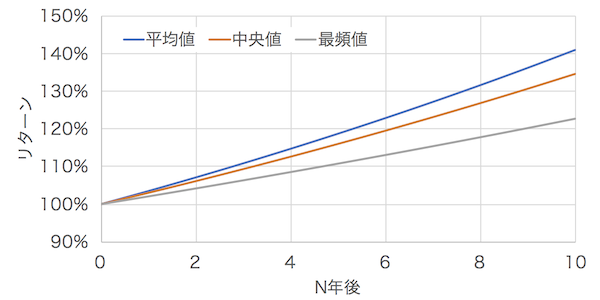
なんとリスクを下げると、平均値と中央値が近づきました。さらに最頻値がプラスに転じています。リターンの平均値は下がっていますが、プラスになる可能性が高くなったということです。
平均値(期待値)をアテにすると誤る可能性がある
さて、数学的な確率を見てきました。ここからわかることは、期待値だけを計算すると大きくミスする可能性があるということです。サンクトペテルブルクのパラドックスでは期待値が無限大になる例を示しました。その後の例では、平均値は高いが、中央値と最頻値がそれを下回る例を出しました。これは似たことを示していて、一部の結果が平均値を大きく押し上げているが、多くの場合は平均値に届かないということです。
ぼくらが投資をする場合、期待値と中央値、最頻値のどれを指標にするべきでしょうか? 期待値(平均値)が意味をもってくるのは、試行頻度が多いときです。サンクトペテルブルクのパラドックスの場合でも、試行頻度が10億回などに達すれば1回あたり最低10円は稼げることが分かりました。ただし、試行頻度が少ないと、期待値は無限大でもほとんどの場合で稼げる額は小さいままです。
投資でも、試行頻度を増やせるならば、期待値が意味を持ってくるのではないかと思います。逆に、長期投資のように試行頻度が1回に近い場合は、期待値だけを見るのは危険です。
特に、老後を考えた場合、平均してどうか、ではなく自分がどうなるかが大事です。つまり、少なくとも元本割をしない可能性を高めることが大事ですし、もし10回繰り返せたとしたら5回はうまくいく可能性(中央値)を見たほうがよいでしょう。中には、とんでもなく大きく資産を増やせる可能性もありますが、長期投資でそれに賭けるのはリスキーだと思います。
モンテカルロ・シミュレーションでも確かめる
長期で資産運用したときに、期待値だけでなく中央値、最頻値をしっかりと表示してくれるサービスもあります。ファンドの海が提供している長期投資予想/アセットアロケーション分析がその1つです。
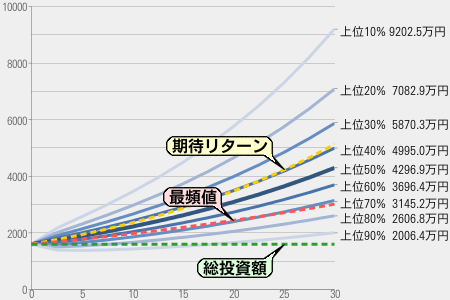
上位何パーセントがどこまでに収まっているかを確率分布を元に計算してくれます。
確率分布の計算だけでなく、乱数を発生させてどんな結果になるかを表示するサービスも試すとよいでしょう。ぼくのサイトで作成した九条日記セミリタイアシミュレーターもその1つです。
