『適応的市場仮説』からのお話も、今回が最後。「確率マッチング」という不思議な判断についてです。
確率マッチングとは?
まず人間心理の不思議を見てみましょう。シンプルなゲームです。このゲームをすると、AかBのどちらかの結果が出ます。事前にどちらが出るか予測して、当たっていたらドルもらえ、外れたら1ドル取られます。このゲームを複数回繰り返すとしましょう。
もしAとBが同じ確率で出るなら期待値はゼロですね。 では、75%の確率でA、25%の確率でBだったらどうするでしょうか?

例えばこのゲームを100回やるとします。このとき、常にAを出し続ければ当たる確率は75%、つまり獲得期待値は75ドルです。そして外れる確率は25%、つまり損失期待値は25ドル。合計すると50ドルが、このゲームの期待値です。
なぜか人は確率に従って手を選ぶ
このゲームをAが出る確率を知らせずにプレーヤーにやらせるとします。ゲームを続けるうちに、「なんとなくAのほうが多く出ているぞ」と気づきます。数十回繰り返せば、4回のうち3回はAが出て、Bは1回くらいしか出ないということが肌感覚で分かるでしょう。
ではこのとき、プレーヤーはABどちらをどのような比率で出すでしょうか?
答えは数学で簡単に出る。オッズについて何も聞かされていないとして、何回かプレイしてAのほうがBよりよく現れるにの気づいたら、累計の儲けを最大化するにはいつも「A」のキーを押していればいい。Aが出るのを当てる可能性はBが出るのを当てる可能性より常に大きい。
正しい答えはこれなのだが、ほとんどの人はそうしない。
そうなのです。ではどうするのか。実は「Aを約75%、Bを約25%の割合で押す」という戦略を取ったのです。これを心理学者は「確率マッチング」といいます。
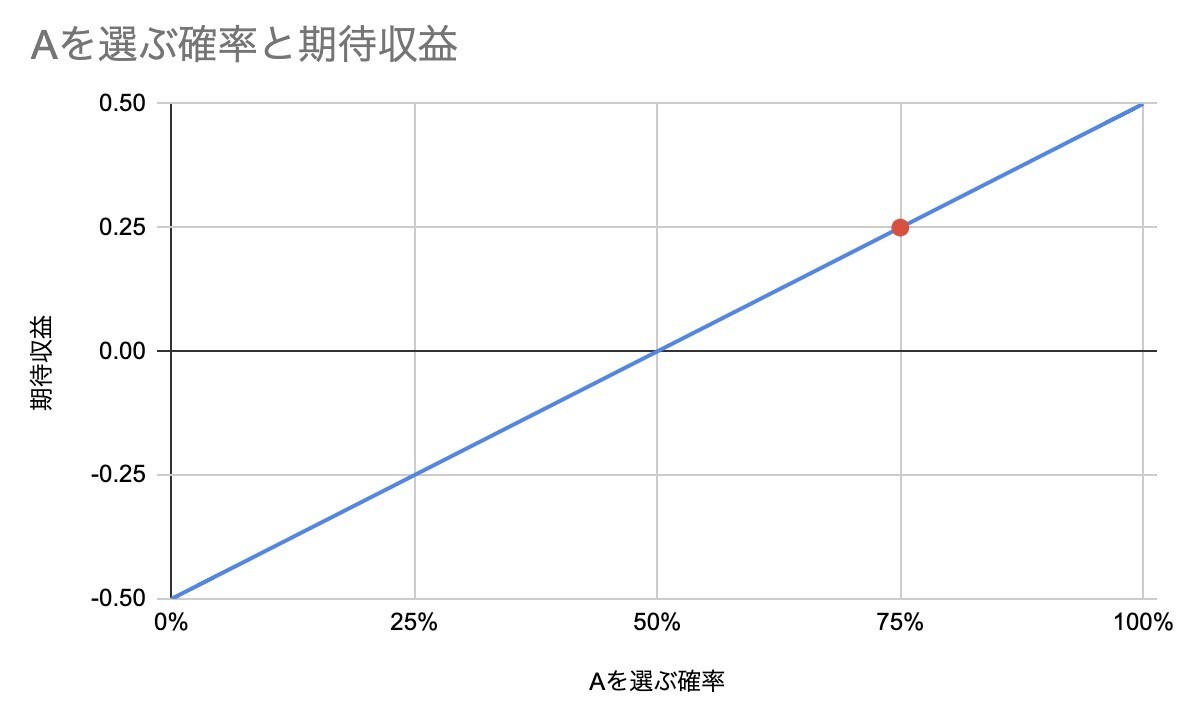
念の為、このゲームでAを選ぶ確率を変化させたときに、1回あたりの期待収益がどうなるのかを計算したグラフがこちらです。よくよく考えれば当然なのですが、毎回Aを選べば期待収益は(0.75ドル-0.25ドル)で0.5ドルになります。ところが、Aを75%の確率で出した場合、期待収益は(0.63ドルー0.37ドル)の0.25ドルにしかならないのです。半分になってしまいます。
脳の奥に刻まれた確率マッチング
これだけなら、「あー、人は合理的じゃないんだね」で終わる話です。片方の確率が大きいなら、常にそれを出し続けるのが合理的なのに、つい、その出現確率に合わせる形で別の手も混ぜてしまうのです。
株価が上がる確率が70%で下がる確率が30%なら、常に上がるほうに賭けるほうが勝率は高いのですが、つい、7割の手はロングで3割ショートしてしまうという感じです。
しかし、脳の仕組みを解明していく中で不思議なことが起こりました。右脳と左脳の違いについては、よく知られています。論理的な左脳に対して感情的な右脳とよくいわれますね。そして右目は左脳に、左目は右脳にクロスしてつながっています。
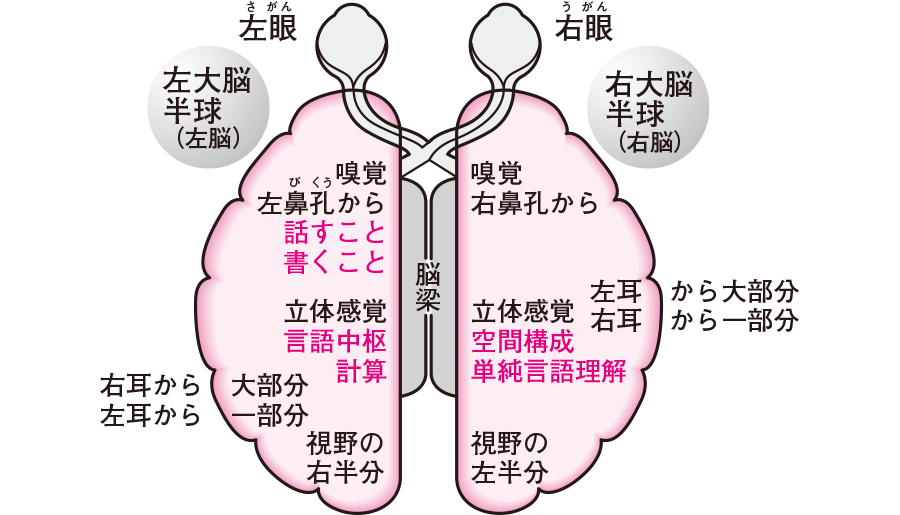
この右脳と左脳をつないでいるのが脳梁です。ところが以前、てんかんの治療のために、脳梁を切断するという手術が行なわれました。そうなった「分離脳」と呼ばれる人は、右脳と左脳で連携できず、まるで別の人格のように振る舞うのです。
さてここからが本題。 この分離脳の人に、先のゲームをさせるとどうなるか?
分離脳の被験者に右目だけでゲームをさせると彼らは確率マッチングを行い、左目だけで見させると彼らは最適な戦略を割り出して100%の割合で「A」を選んだ。(中略)
右目につながった「合理的な」左脳は確率マッチングを行い、左目につながった「感情的な」右脳は最適な戦略を選んだ。
『適応的市場仮説』p168
あら不思議。右目→左脳で見てプレイした人は、通常通り確率マッチングを行ったのですが、左目→右脳でプレイした人はなんと、100%の確率でAを選んだというのです。一般に、左脳は合理的で、右脳は感情的だといいますが、本当に合理的な戦略を選んだのは右脳でした。
さらに不思議は続きます。この確率マッチングゲームの見せ方をちょっと変えて、文字ではなく顔で行うと、右脳も「確率マッチング」をやりだしたというのです。
確率マッチングゲームを文字ではなく顔でやると、右脳はもう最適な答えを出さず、代わりに確率マッチングをやりだした。
この不思議な現象は次のように説明されています。
右脳は、現実のいつ、どこで、誰が、何を――奥さん、事実だけをお願いします――を担い、一方左脳は、どうやって、それに、なぜ、を推し量るのを担うと結論付けた。左脳はこの仕事を華麗にやってのける。観測したデータに合う物語を作り上げるのだ。
なるほど、左脳は合理的だというよりも、物語を作り上げる、因果を勝手に構築する仕事をしているのだというのです。一方で、物語を構築する能力は、私たちが「知性」と呼ぶものの核です。私たちは世界を事実である物事ではなく、物語の流れとして認識しているからです。
進化における確率マッチング
実は本書『適応的市場仮説』の主題は、この確率マッチングに密接に結びついています。なぜ一見非合理的な確率マッチングが起きるのかを、筆者は次のような思考実験で解き明かそうとしています。
架空の宇宙生物「トリブル」が、谷と台地の2種類の地形しかないところで暮らしています。一生に一度だけ繁殖し、うまくいけば3匹の子孫を残し、やがて死にます。繁殖に交配は必要ありません。トリブルは短い人生の中で一度だけ大きな決断を下します。巣を谷と台地のどちらに作るか? です。
日が照っている場合、谷に巣を作るのが理想的で、日差しを避け谷の川から水が手に入ります。そのため、3匹の子孫は生き残ることができます。ところが、このとき岩だらけの台地に巣を作ると日差しと水不足で子孫は全部死んでしまいます。
一方、雨がふると状況はひっくり返ります。谷にいるトリブルの子孫は鉄砲水で死んでしまいます。台地にいれば洪水もなく、雨雲が日差しを遮るため3匹の子孫は生き残ります。
ではここで、日照りの確率を75%、雨の確率を25%とした場合、トリブルが子孫の数を最大化するために最適な戦略はどうなるでしょうか? はい。これは確率マッチングゲームですね。毎回谷に巣を作れば、子孫が生き残る確率は最大(75%)になります。

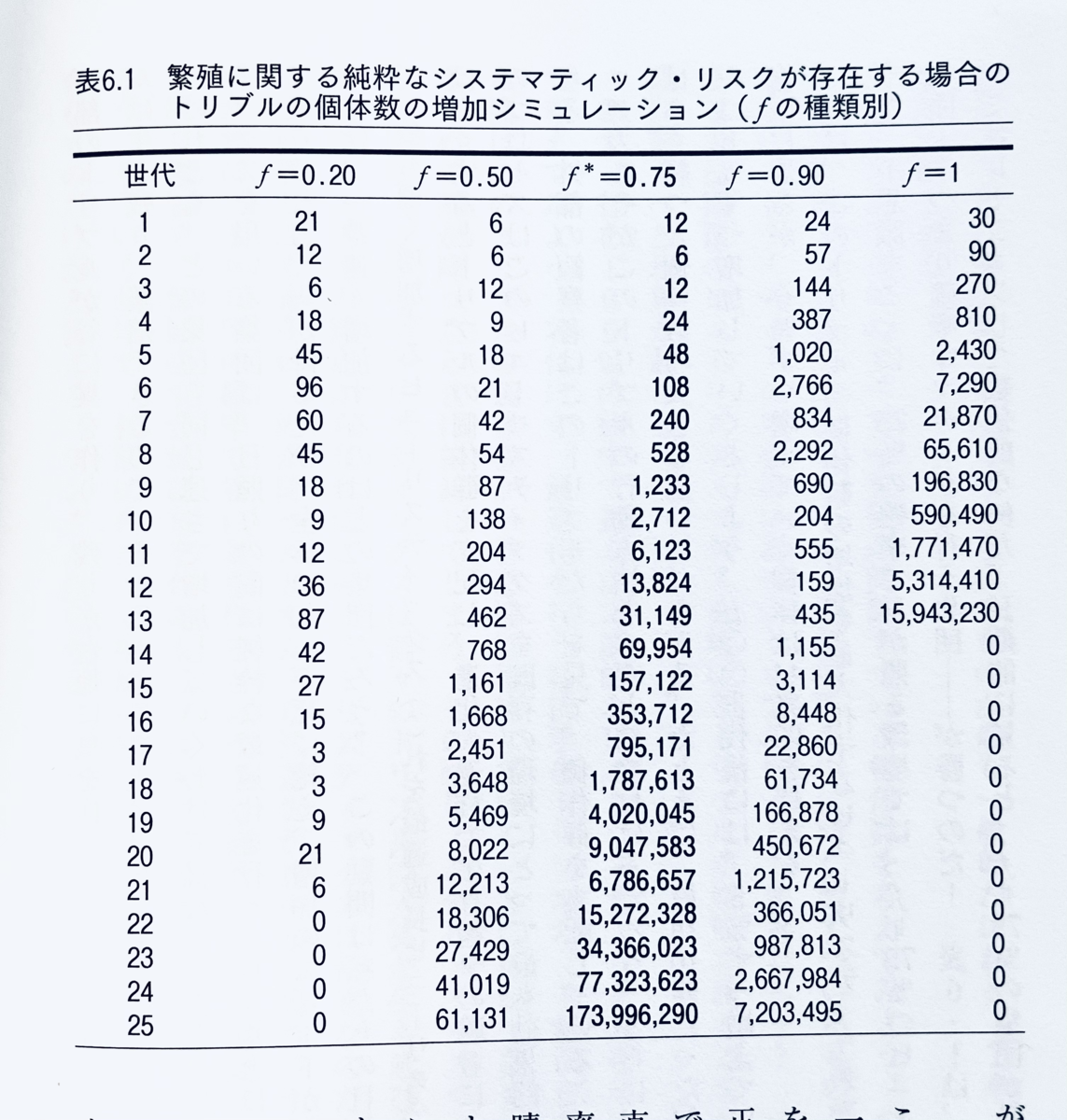
ところが、ここにさまざまなトリブルの部族がいるとしましょう。部族ごとに方針があって、一定の確率で谷を選ぶとします。例えば、80%の確率で谷、20%の確率で台地というような感じです。このとき、部族ごとの子孫の数はどう変化するでしょうか?
まず一見合理的な毎回谷に巣を作る(谷=100%)の部族から。名付けて最適化を行う経済学者トリブルです。
予想にたがわず、日照りが続いている間は、このトリブルの個体数が一番急速に増加していく。ところが、全員が谷に巣を作るものだから、はじめて雨が降ったときに絶滅してしまう。
なるほど、個々のトリブルの選択としては、谷=100%は最適解なのですが、進化の観点からみれば持続可能ではないということです。雨が降った途端この最適化トリブルは全滅してしまい、遺伝子は後世に残りません。
というわけで、谷=100%ではなく、ランダムに谷と台地に分けて巣を作る部族しか、長期的には生き残れないのです。では、どのようなランダムがベストなのでしょうか。
不思議なことに、75%の確率で日が照る場所では、谷=75%の確率で巣を作る集団――すなわち確率マッチング行う部族――が勝つのだ!
投資における確率マッチング
このように、ある条件のもとでは、一見合理的な確率を最大化しようとする戦略が全滅し、一見非合理な確率マッチングが生き残って繁栄します。これはどんな条件が影響しているのでしょうか。
先程の実験では「雨がふると谷に済むトリブルがいっせいに死んでしまう」と仮定していました。しかし、雨がふるのも確率的に決まるように条件を変えるとどうなるでしょうか。どの場所でもすべてに雨(確率75%)、すべてが晴れ(確率25%)、ではなく、75%の場所が雨、25%の場所が晴れとしてみるのです。
このたったひとつの環境の変化が及ぼす影響は、ものすごく大きい。局所的に天候が変わる世界では、最適化を行う経済学者トリブル――つまり、常に期待される子孫の数を最大化しようとするトリブル――が最も急速に増加する。
どうして?理由はごくごく単純だ。経済学者トリブルが全滅する可能性は限りなくゼロに近いからだ。
p.287
こういう条件の元では、トリブルは最も合理的な選択をする部族に席巻されてしまうでしょう。では、これを現実に当てはめてみるとどうなるでしょうか。
2つ目の例では、75%のトリブルには雨がふり、25%のトリブルは晴れでした。このようなリスクを「固有リスク」と呼びます。一方、最初の例では確率75%で雨が降ると、すべてのトリブルが雨の影響を受けました。この「すべての固体に同じリスクが及ぶ」ことを、金融経済学者は「システマティックリスク」と呼びます。
システマティック・リスクが存在する場合、全員が同じ行動を取るのは――たとえば全員が谷に巣を作るのは――持続可能な行動とは言えない。(中略)
この種の環境では、ランダム化した行動を用いるヒューリスティックスが最もうまくいく。その中でも最も効果的なのは確率マッチングのヒューリスティックスだ。
p.288
なるほど、現在の人間が自然と確率マッチングを取ってしまうのは、地球上の環境に少なからず「システマティックリスク」が存在しており、完全に合理的で最適な戦略をとった人間の子孫は、どこかで全滅してしまったから、だというわけです。
例えば、株式Aと株式Bがあって、A株のパフォーマンスは75%の確率でB株より高く、A株が上がるとB株が下がるという関係にあるとします*1。
合理的に考えると、A株は常にB株よりも基本的にパフォーマンスが高いので、すべてA株を持つことが最適解になります。ところが、A社に不祥事が発覚して倒産してしまいました。すると、A株だけを持っていた投資家は退場することになってしまいます。A株を保有している投資家全員にとって、倒産はシステマティックリスクだったということです。このような状況では、A株を75%、B株を25%持つことが(確率マッチング)、生き残るためには必要だということです。
このように、生物学や環境変化による進化のプロセスも考慮に入れて、著者は「適応的市場仮説」を打ち立てました。
適応的市場仮説は、人間に合理性や非合理性を与える条件を提示する。そして、自然選択が私たちの行動に魔法をかけている間、合理性と非合理性がしばらく共存することもありえるのだ。
本書は注を除いても600ページを超える大部であり、金融工学の歴史から基礎、そして生物学、実際のヘッジファンドのあり方(筆者自身もヘッジファンドの運営者)まで、多岐に渡る話題が満載の本です。ある程度基礎的なことを知っていたほうが楽しく読めると思いますが、基本的には物語であり、例示が中心で、数式は出てきません。久々に興奮する金融読み物に出会えた感じです。
*1:ちなみに投資でいうシステマティックリスクとは、一般に、ポートフォリオを分散化させても消去できないリスクのことを指します。この時、A株とB株の両方を持てば、株固有のリスクは打ち消し合って消滅します。これはいわゆるポートフォリオ理論の基礎ですね。一方で、A株もB株も、例えばコロナショックのようなときには一律に下落します。これは両方の株を分散して持っていても打ち消せないリスクなので、システマティックリスクだというわけです。固有リスクの範囲と、システマティックリスクの範囲が少し異なることに注意が必要です
