行動経済学の概念の1つに「損失回避効果」というものがあります。プロスペクト理論の1つで、「ヒトは利益を得られることよりも、損失を忌避する傾向が強い」ことを指します。
そりゃそうだよね、と思うかもしれません。ところが、一歩踏み込んで見ていくと、条件によっては不思議なパラドックスも生まれるのです。大部の投資本『適応的市場仮説』の一節より。
損失回避効果の例――アルファとブラヴォ
結果にリスクが伴う選択を行うとき、私たちの大部分は利益より損失を重視する。リスクがある状況では、私たちは単純な数学が予測するよりも、ずっと損失を嫌う態度を示す。
これは、「得」を得ることよりも「損」しないことを重視しがちだという意味です。具体的なサンプルで見てみましょう。アルファ・リミテッド(A)とブラヴォ・インク(B)の2社への投資を考えているとします。条件は次のとおりです。
- アルファ・リミテッド 確実に24万ドル儲かる
- ブラヴォ・インク 25%:100万ドル儲かる 75%:ゼロ
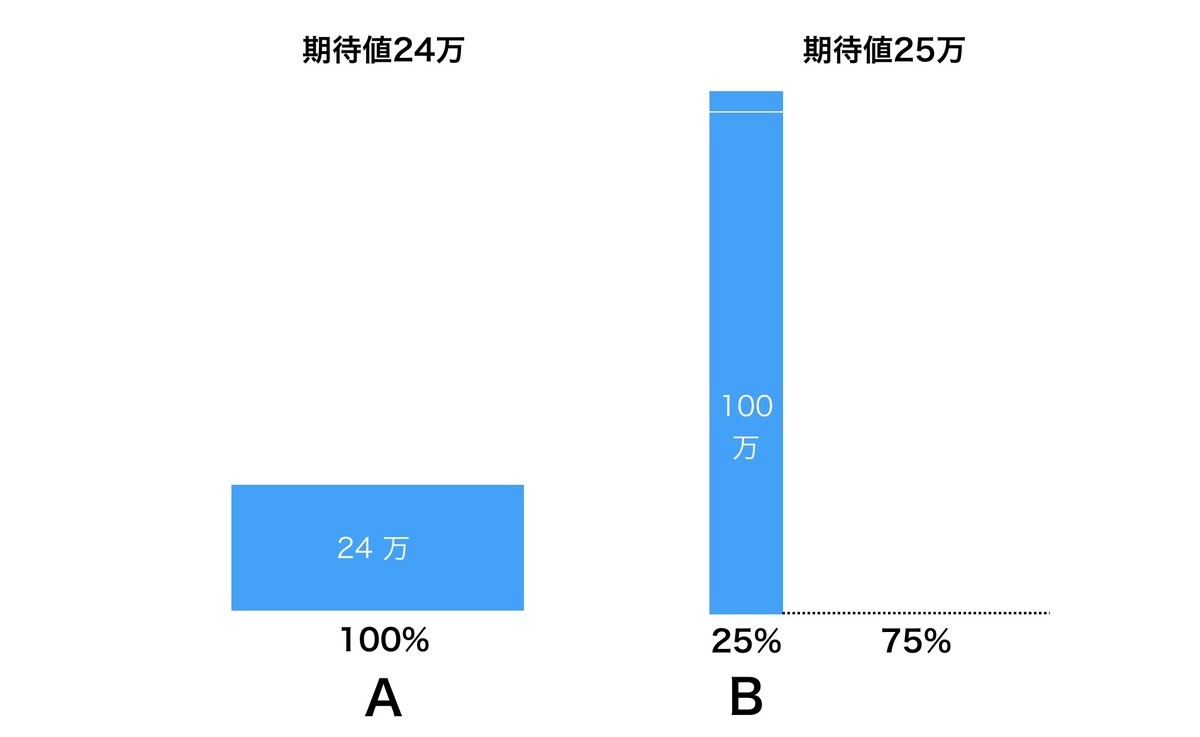
図にするとこんな感じ。横軸が確率で縦軸が得られる金額です。面積が期待値だと考えるといいでしょう。このような選択があったとき、多くの人はAのアルファを選びます。期待値は1万ドル少ないのに、です。確実な24万ドルのほうを選好する人が多いということです。
損失回避効果の例――チャーリーとデルタ
ではこのような条件ではどうでしょう? 確実に損をするチャーリー(C)と一定の確率で損失を免れるデルタ(D)です。
- チャーリー・カンパニー 確実に75万ドル損する
- デルタ・コーポレーション 25%:ゼロ 75%:100万ドル損
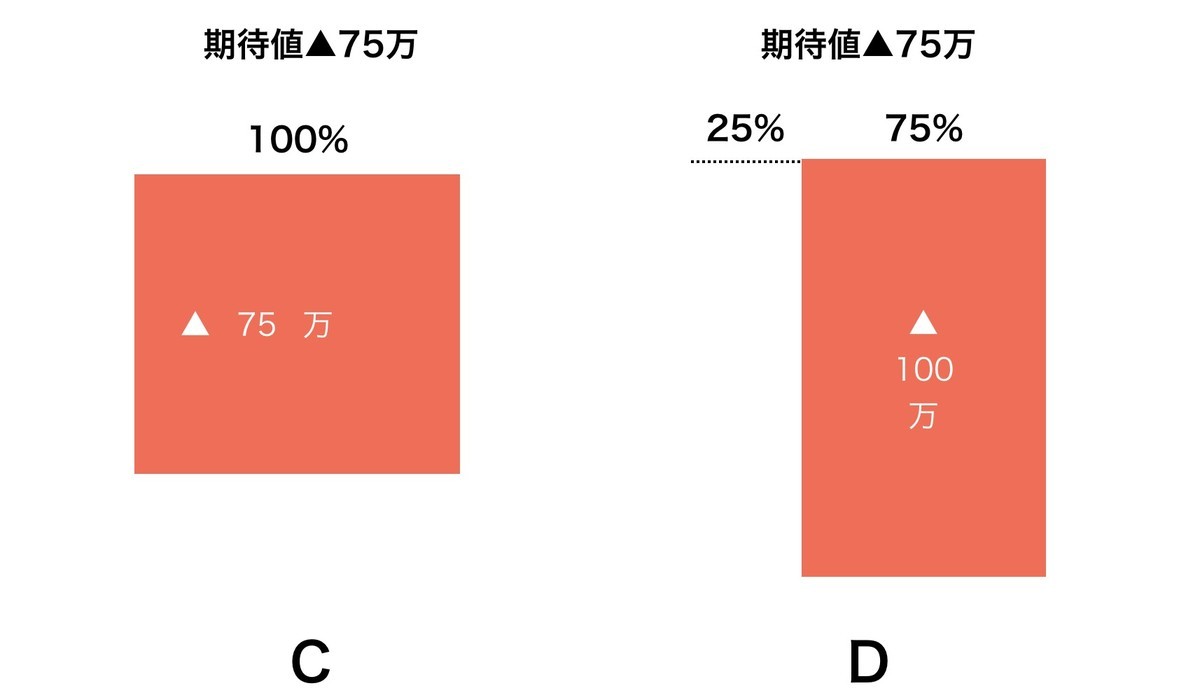
今度は一転して、 確実な損失よりも、損失ゼロの可能性があるDのほうを選ぶ人が増えます。期待値は同じマイナス75万ドルなのに、確実性よりもリスクがあってもゼロの可能性を選ぶわけです。
4つの例のミックスを考える
「そりゃ、儲かるかどうか運次第よりも、確実に儲かるほうがいいし、確実に損をするよりは損しない可能性があるほうがいいよね」。そう思うかもしれません。別に不合理ではない。誰でもそうでしょ? と思いがちです。
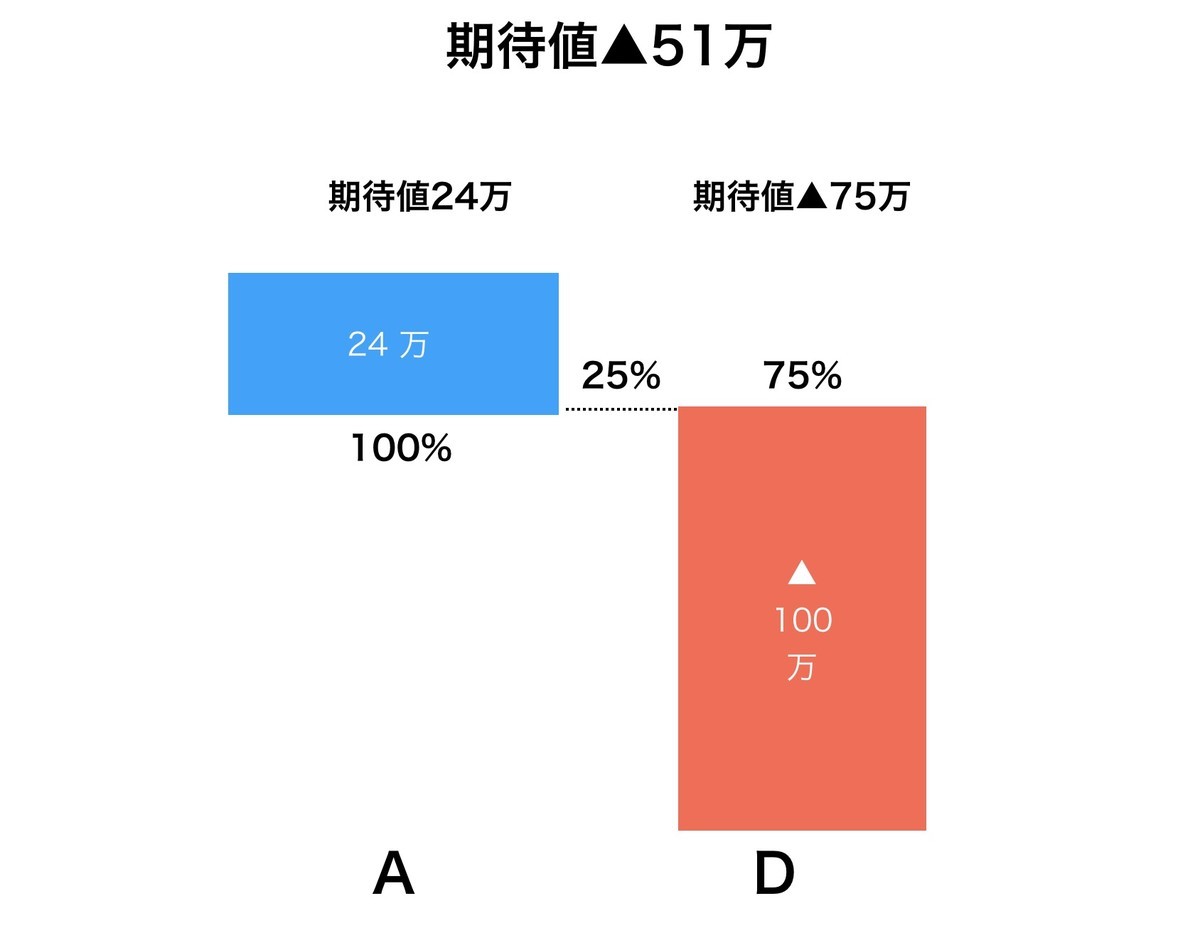
では今度は、これらの組み合わせを考えます。それぞれの選択で、最も人気のあった、アルファ(A)とデルタ(D)を組み合わせるとどうなるでしょうか。合計すると、25%の確率で24万ドル儲かり、75%の確率で76万ドル損する形になります。期待値はマイナス51万ドルです。
では逆に、それぞれの選択で不人気だったブラヴォ(B)とチャーリー(C)の組み合わせはどうなるでしょうか? こちらは25%の確率で25万ドル儲かり、75%の確率で75万ドル損する形です。期待値はなんとマイナス50万ドル。
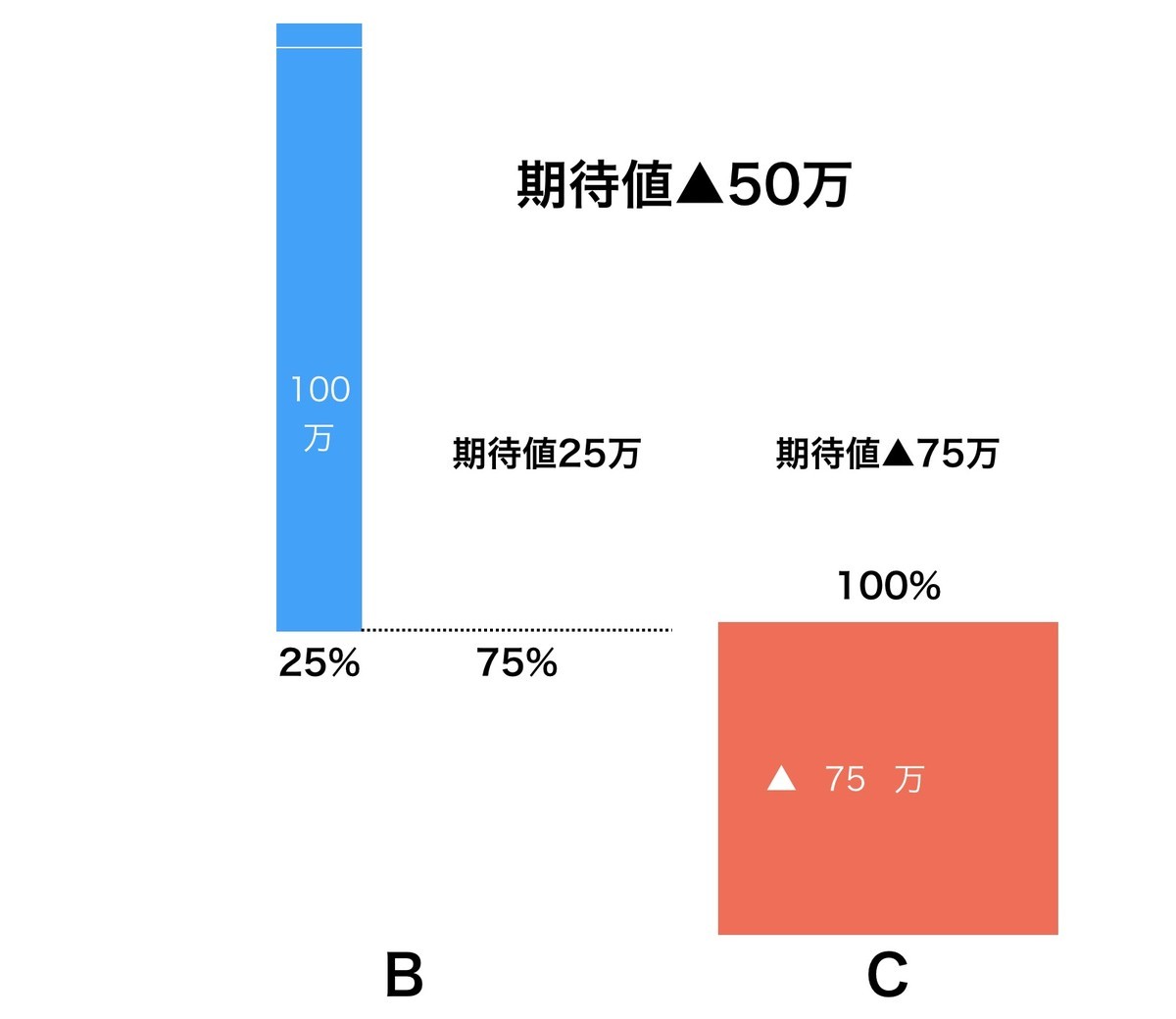
驚いたことに、2つを組み合わせると、合計した確率と損益は次のようになるのです。
- A+D 25%の確率で24万ドル儲かる 75%の確率で75万ドル損する
- B+C 25%の確率で25万ドル儲かる 75%の確率で75万ドル損する
いずれも儲かる確率は同じ25%、損する確率も同じ75%。ところが、儲かるときの額は不人気だったB+Cのほうが1万ドル高いのです。
損失回避の行動が不合理をもたらす
このように、ひとつひとつの意思決定だけを見ると、損失回避のための選択は「そんなにおかしくない」ようにも見えます。ところが、それらを複数組み合わせた場合、個別個別の意思決定の積み重ねが、不合理な結論につながってしまうのです。
このような形は、株式投資でもしばしばありますね。含み益が乗ったらそれが小さくでも利確したくなるのは「確実な利益」を得たいという損失回避効果のためですし、含み損が出たら一発逆転を狙って塩漬けにしたくなるのも損失回避のなせる技です。ところが、そうした選択を積み重ねると、合計では、先の例のように、あれ? 全体として損してるぞ? となるのでしょう。
いやはやお金にまつわる人間の心理は面白いものです。
